Menelaus' Theorem Proof

Proposition
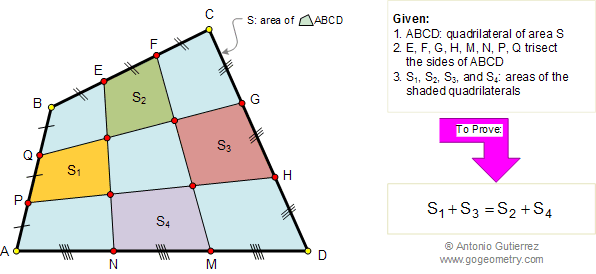
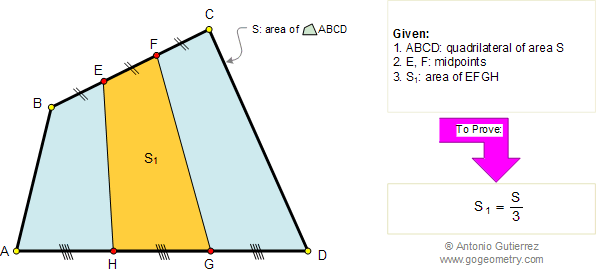
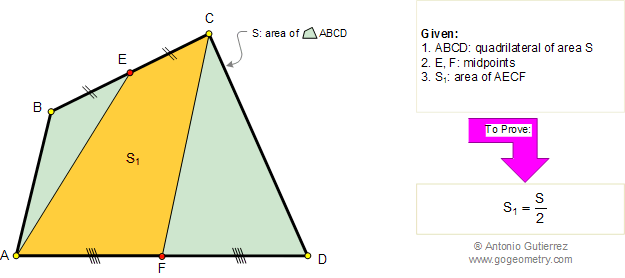
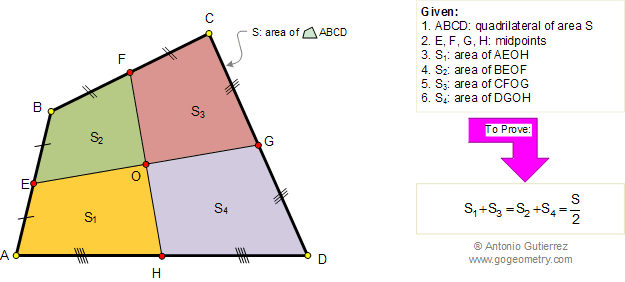
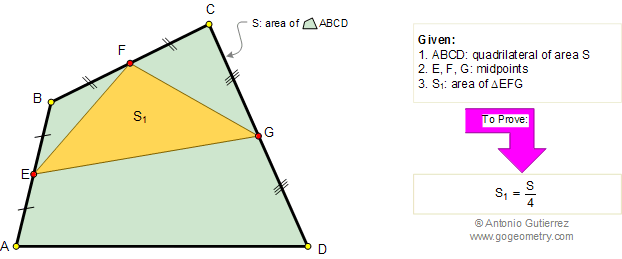
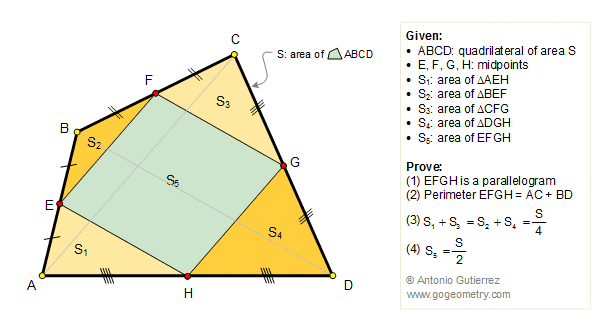
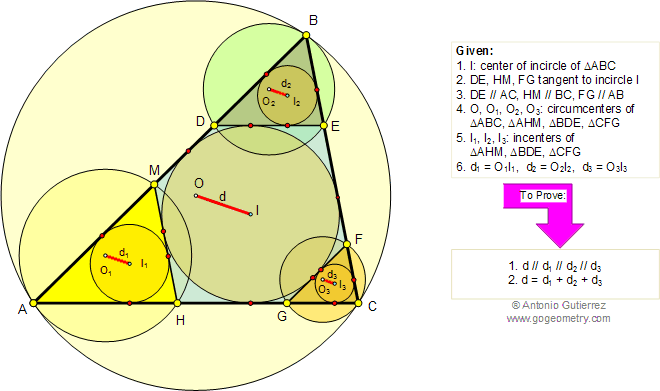
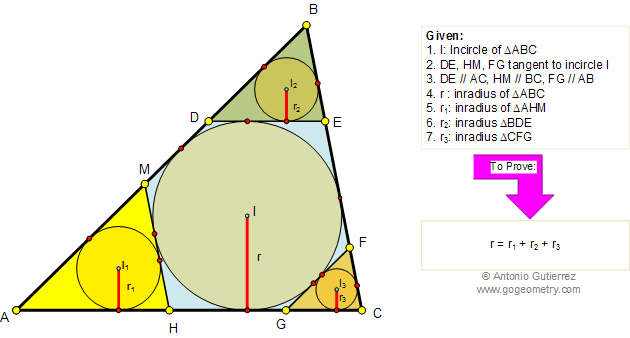
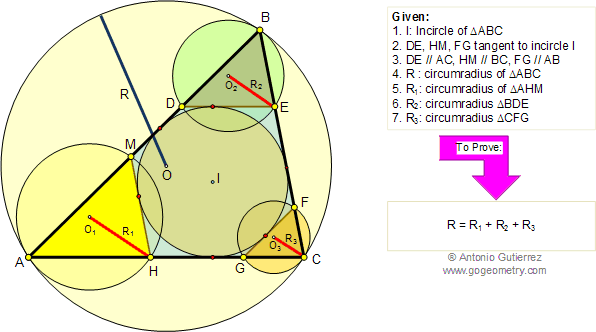
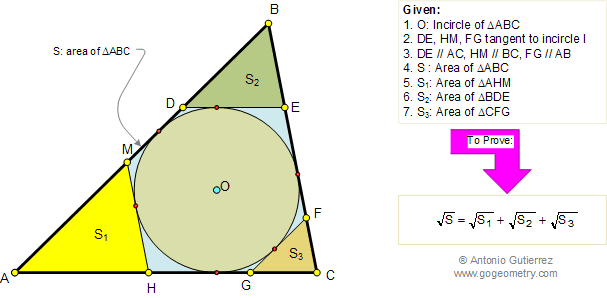
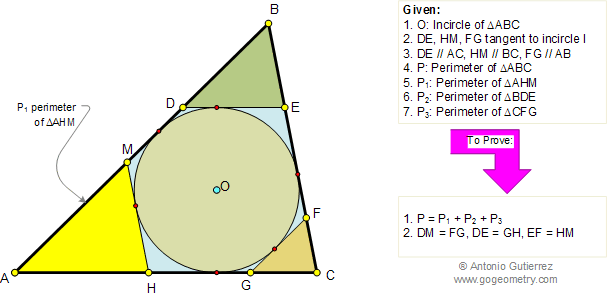
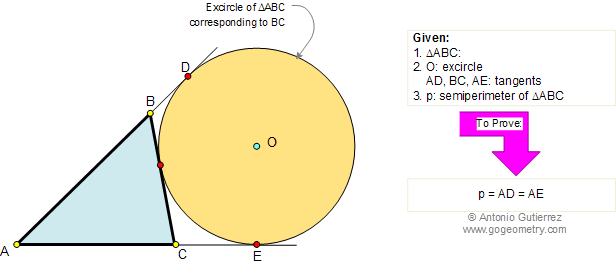
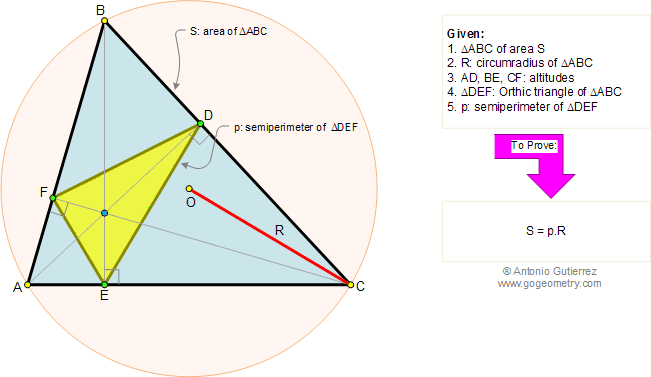
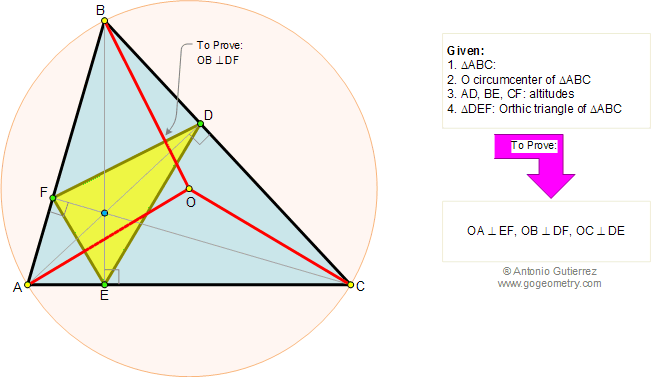
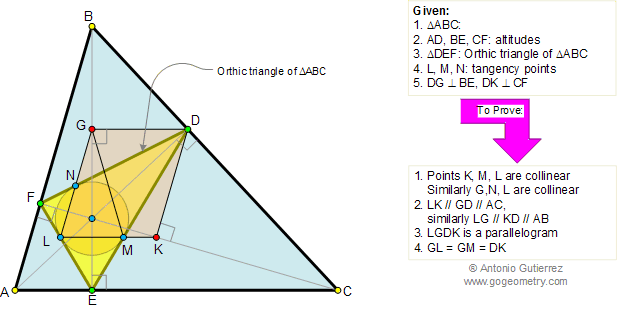
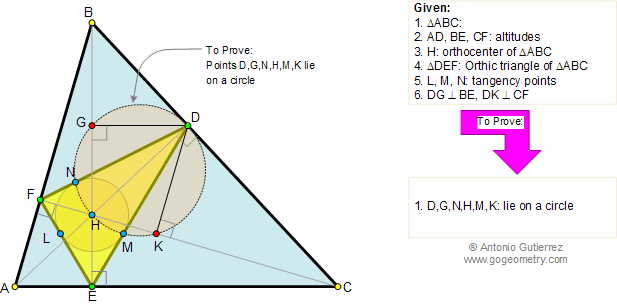
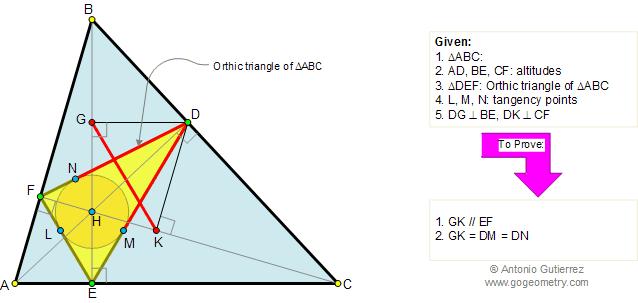
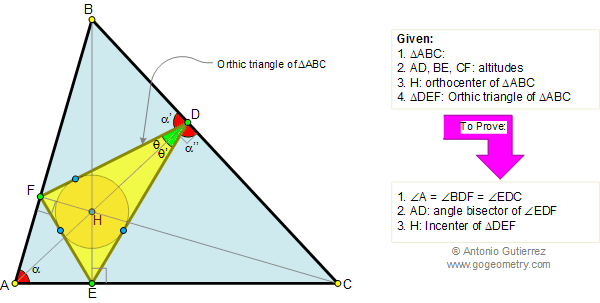
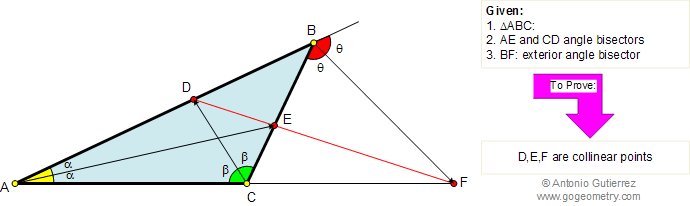
Let ABC be a triangle and MEN a line that transverse (crosses) the lines AB, BC, and AC respectively. Prove that (AM.BE.CN)/(MB.EC.NA)=-1. The converse also holds.



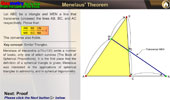
See complete interactive proof with animation and key concepts
Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Elearn Geometry Problem 151

See complete Problem 151
Quadrilateral, Area, Trisection of Sides. Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Elearn Geometry Problem 150

See complete Problem 150
Quadrilateral, Area, Trisection of Sides. Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Elearn Geometry Problem 149

See complete Problem 149
Quadrilateral, Area, Midpoints. Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Elearn Geometry Problem 148

See complete Problem 148
Quadrilateral, Area, Midpoints. Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Elearn Geometry Problem 147

See complete Problem 147
Quadrilateral, Area, Midpoints, Triangle. Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Elearn Geometry Problem 146 Varignon s theorem and more

See complete Problem 146
Varignon's Theorem: Quadrilateral, Midpoints, Parallelogram, Area, Perimeter. Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Elearn Geometry Problem 145

See complete Problem 145
Four Triangles, Incircle, Tangent and Parallel to Side, Incenters, Circumcenters. Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Elearn Geometry Problem 144

See complete Problem 144
Four Triangles, Incircle, Tangent and Parallel to Side, Circumradii. Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Elearn Geometry Problem 143

See complete Problem 143
Four Triangles, Incircle, Tangent and Parallel to Side, Circumradii. Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Elearn Geometry Problem 142

See complete Problem 142
Four Triangles, Incircle, Tangent and Parallel to Side, Areas. Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Elearn Geometry Problem 141

See complete Problem 141
Triangle, Incircle, Tangent and parallel to side, Perimeter. Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Elearn Geometry Problem 140

See complete Problem 140
Triangle, Excircle, Tangent, Semiperimeter. Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Elearn Geometry Problem 139

See complete Problem 139
Triangle Area, Orthic Triangle, Semiperimeter, Circumradius. Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Elearn Geometry Problem 138 Nagel's Theorem

See complete Problem 138
Nagel's Theorem, Orthic Triangle, Altitudes, Circumradius, Perpendicular. Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Elearn Geometry Problem 137

See complete Problem 137
Orthic Triangle, Altitudes, Perpendicular, Incircle, Collinear Points, Parallelogram. Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Elearn Geometry Problem 136

See complete Problem 136
Orthic Triangle, Altitudes, Orthocenter, Incenter, Perpendicular, Concyclic Points. Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Elearn Geometry Problem 135

See complete Problem 135
Orthic Triangle, Altitudes, Perpendicular, Parallel. Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Elearn Geometry Problem 134

See complete Geometry Problem 134
Orthic Triangle, Altitudes, Angle Bisectors, Orthocenter, Incenter. Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Pappus Theorem

Proposition
If six points 1,2,3,4,5, and 6, on two lines are joined as shown, then their points of intersection A, B, and C are collinear.



See complete interactive figure
Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Gergonne Line

Proposition
Given a triangle ABC, D, E, and F are the points of contact of the incircle with the sides, as shown. AC and DF meets at B', BC and EF meets at A', and AB and DE meets at C'. Prove that A', B', and C' are collinear.

The line A'B'C' is called Gergonne Line and the points A',B'C' are called Nobbs' points.



See complete interactive figure
Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Interactive Simson Line

Proposition
Given a triangle ABC and P a point on its circumcircle, as shown. Prove that the feet D, E, and F of the perpendiculars drawn from P to the sides (or their extensions) are collinear. The line DEF is called the Simson line.



See complete interactive figure
Triangle, Circumcircle, Perpendiculars, Collinear feet points. Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Triangle, Medians, Six Circumcenters Concyclic

Proposition
Medians AD, BE, and CF split a triangle ABC into six smaller triangles. Prove that their circumcenters O1, O2, O3, O4, O5, and O6 are concyclic (lie on a circle).



See complete interactive figure
Triangle, Medians, Six Circumcenters Concyclic. Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Trapezoid, diagonal, midpoints

Proposition
Given a triangle ABC and a trapezoid ADEC (DE // AC), as shown. AE and CD meet at F, and BF meets DE and AC at N and M respectively. Prove that M and N are the midpoints of AC and DE respectively.



See complete Problem
Trapezoid, Triangle, Diagonals, Midpoints. Dynamic Geometry.
Step-by-Step construction, Manipulation, and animation.
Prove proposition.. Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Dynamic Geometry: Triangle

See complete Problem at Dynamic Geometry


Triangle: Incircle, Perpendicular, Angle Bisector. Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.

Elearn Geometry Problem 133

See complete Problem 133
Triangle, Angle Bisectors, Collinear Points. Level: High School, SAT Prep, College geometry

Post your solutions or ideas in the comments.