Geometry Problems 531 - 540 Sawayama - Thebault's theorem

Ten Geometry Problems
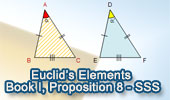
Click the figure below to see problems 531-540 about: Triangle, Circumcircle, Area, Angle Bisector, Midpoint, Parallel, Perimeter, Perpendicular, Euclid Elements, Square, Dissection, Sawayama - Thebault's theorem.

Read more

Level: High School, College geometry

Problem 533: Euclid's Elements Book XIII, Proposition 10

Geometry Problem
Click the figure below to see the complete problem 533 about the sides of the regular pentagon, regular hexagon and regular decagon inscribed in the same circle.


See also:
Complete Problem 533

Level: High School, SAT Prep, College geometry

Raphael's Fresco of the School of Athens - Video by Columbia University

Video and News
Masterpieces of Western Art at Columbia University has been a degree requirement for all College students and an integral part of the Core Curriculum since 1947.

For a 2D symmetry group, a kaleidoscopic point is a point of intersection of two or more lines of reflection symmetry.
Click the figure below to see the illustration.


Continue reading at:
The School of Athens, Columbia University

The School of Athens by Raphael

Pythagoras, Euclid, Socrates, Plato, Aristotle and more together!
Click the figure below to see the illustration.


Continue reading at:
The School of Athens

Euclid's Elements Book I, Proposition 8: (Side-Side-Side SSS Congruence)

If two triangles have the two sides equal to two sides respectively, and have also the base equal to the base, they will also have the angles equal which are contained by the equal straight lines.
Click the figure bellow to see the illustration.



Read more at:
Euclid's Elements Book I, Proposition 8

Euclid's Elements Book I, Proposition 7

Given two straight lines constructed on a straight line (from its extremities) and meeting in a point, there cannot be constructed on the same straight line (from its extremities), and on the same side of it, two other straight lines meeting in another point and equal to the former two respectively, namely each to that has the same extremity with it.
Click the figure bellow to see the illustration.



Read more at:
Euclid's Elements Book I, Proposition 7

Euclid's Elements Book I, Proposition 5: (Pons Asinorum)

In isosceles triangles the angles at the base are equal to one another, and, if the equal straight lines are produced further, then the angles under the base will be equal to one another.
Click the figure bellow to see the illustration.



Read more at:
Euclid's Elements Book I, Proposition 5

Euclid's Elements Book I, Proposition 4: SAS

If two triangles have two sides equal to two sides respectively, and have the angles contained by the equal sides also equal, then the two triangles are congruent
Click the figure bellow to see the illustration.



Read more at:
Euclid's Elements Book I, Proposition 4

Euclid's Elements Book I, Proposition 3

Given two unequal straight lines, to cut off from the greater a straight line equal to the less
Click the figure bellow to see the illustration.



Read more at:
Euclid's Elements Book I, Proposition 3

Euclid's Elements Book I, Proposition 2

To place at a given point (as an extremity) a straight line equal to a given straight line
Click the figure bellow to see the illustration.



Read more at:
Euclid's Elements Book I, Proposition 2

Euclid's Elements Book I, Proposition 1

On a given finite line to construct an equilateral triangle
Click the figure bellow to see the illustration.



Read more at:
Euclid's Elements Book I, Proposition 1

Puzzle: Euclid's Elements Book I, 23 Definitions

Interactive Puzzle
Click the figure to solve the interactive puzzle about Euclid's Elements Book I, 23 Definitions.



See also:
Puzzle: Euclid's Elements Book I, 23 Definitions

Euclid's Elements Book IV Word Cloud

Weighted list in visual design.
Click the figure below to see the most common words in the Euclid's Elements Book IV.



Read more at:
Euclid's Elements Book IV Word Cloud

Euclid's Elements Book III Word Cloud

Weighted list in visual design.
Click the figure below to see the most common words in the Euclid's Elements Book III.



Read more at:
Euclid's Elements Book III Word Cloud

Euclid's Elements Book II Word Cloud

Weighted list in visual design.
Click the figure below to see the most common words in the Euclid's Elements Book II.



Read more at:
Euclid's Elements Book II Word Cloud

Euclid's Elements Book I Word Cloud

Weighted list in visual design.
Click the figure below to see the illustration.



Read more at:
Euclid's Elements Book I Word Cloud

Euclid's Elements Book X, Lemma for Proposition 33

Right triangle, Altitude, and Rectangles

Click the figure below to see Euclid's Elements Book X, Lemma for Proposition 33.


See also:
Euclid's Elements Book X, Lemma for Proposition 33.
Euclid's Elements Index.
Geometry Index

Level: High School, SAT Prep, College geometry

Euclid's Elements

Index

Click the figure below to see Euclid's Elements Index.


See also:
Euclid's Elements Index.
Geometry Index

Level: High School, SAT Prep, College geometry

The Abel Prize: Drawing parallels in geometry

Mikhail Gromov has been awarded the Abel Prize for his work making sense of the range of geometries that appeared in the 19th century and he is a worthy successor to the likes of Euclid, Riemann and Gauss, Bolyai and Lobachevsky.





Read more at:
Drawing parallels in Geometry

Euclid's Elements Book I, Proposition 9

To bisect a given angle




Read more at:
gogeometry.com/geometry/euclid_elements_book_i_9_bisect_angle.htm